Legendre polynomials basis functions.
Use as basis functions Legendre polynomials \(P_{n}(x)\) defined on a bounded interval. You need to provide the interval \([a,b]\) on which the basis functions are to be used, and the order of the expansion \(N\) (i.e. the highest order polynomial used). The total number of basis functions is \(N+1\) as the constant \(P_{0}(x)=1\) is also included. These basis functions should not be used for periodic CVs.
Intrinsically the Legendre polynomials are defined on the interval \([-1,1]\). A variable \(t\) in the interval \([a,b]\) is transformed to a variable \(x\) in the intrinsic interval \([-1,1]\) by using the transform function
\[ x(t) = \frac{t-(a+b)/2} {(b-a)/2} \]
The Legendre polynomials are given by the recurrence relation
\begin{align} P_{0}(x) &= 1 \\ P_{1}(x) &= x \\ P_{n+1}(x) &= \frac{2n+1}{n+1} \, x \, P_{n}(x) - \frac{n}{n+1} \, P_{n-1}(x) \end{align}
The first 6 polynomials are shown below
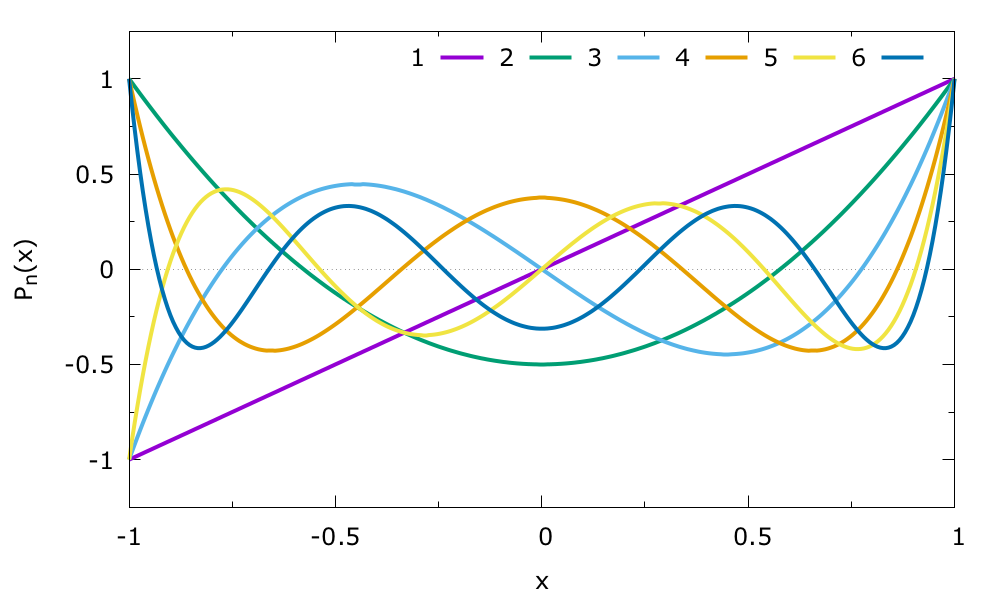
The Legendre polynomial are orthogonal over the interval \([-1,1]\)
\[ \int_{-1}^{1} dx \, P_{n}(x)\, P_{m}(x) = \frac{2}{2n+1} \delta_{n,m} \]
By using the SCALED keyword the polynomials are scaled by a factor of \( \sqrt{\frac{2n+1}{2}}\) such that they are orthonormal to 1.
From the above equation it follows that integral of the basis functions over the uniform target distribution \(p_{\mathrm{u}}(x)\) are given by
\[ \int_{-1}^{1} dx \, P_{n}(x) p_{\mathrm{u}}(x) = \delta_{n,0}, \]
and thus always zero except for the constant \(P_{0}(x)=1\).
For further mathematical properties of the Legendre polynomials see for example the Wikipedia page.
Here we employ a Legendre expansion of order 20 over the interval -4.0 to 8.0. This results in a total number of 21 basis functions. The label used to identify the basis function action can then be referenced later on in the input file.

bf_leg: BF_LEGENDREMINIMUM=-4.0compulsory keyword The minimum of the interval on which the basis functions are defined.MAXIMUM=8.0compulsory keyword The maximum of the interval on which the basis functions are defined.ORDER=20compulsory keyword The order of the basis function expansion.
| ORDER | The order of the basis function expansion. |
| MINIMUM | The minimum of the interval on which the basis functions are defined. |
| MAXIMUM | The maximum of the interval on which the basis functions are defined. |
| DEBUG_INFO | ( default=off ) Print out more detailed information about the basis set. Useful for debugging. |
| NUMERICAL_INTEGRALS | ( default=off ) Calculate basis function integral for the uniform distribution numerically. Useful for debugging. |
| SCALED | ( default=off ) Scale the polynomials such that they are orthonormal to 1. |