BF_CUBIC_B_SPLINES

	This is part of the ves module
	It is only available if you configure PLUMED with ./configure –enable-modules=ves . Furthermore, this feature is still being developed so take care when using it and report any problems on the mailing list.

Cubic B spline basis functions.

Attention

These basis functions do not form orthogonal bases. We recommend using wavelets (BF_WAVELETS) instead that do for orthogonal bases.

A basis using cubic B spline functions according to [59]. See [97] for full details.

The mathematical expression of the individual splines is given by

\begin{align*} h\left(x\right) = \begin{cases} \left(2 - \lvert x \rvert\right)^3, & 1 \leq \lvert x \rvert \leq 2\\ 4 - 6\lvert x \rvert^2 + 3 \lvert x \rvert^3,\qquad & \lvert x \rvert \leq 1\\ 0, & \text{elsewhere}. \end{cases} \end{align*}

The full basis consists of equidistant splines at positions \(\mu_i\) which are optimized in their height:

\begin{align*} f_i\left(x\right) = h\left(\frac{x-\mu_i}{\sigma}\right) \end{align*}

Note that the distance between individual splines cannot be chosen freely but is equal to the width: \(\mu_{i+1} = \mu_{i} + \sigma\).

The ORDER keyword of the basis set determines the number of equally sized sub-intervalls to be used. On the borders of each of these sub-intervalls the mean \(\mu_i\) of a spline function is placed.

The total number of basis functions is \(\text{ORDER}+4\) as the constant \(f_{0}(x)=1\), as well as the two splines with means just outside the interval are also included.

As an example two adjacent basis functions can be seen below. The full basis consists of shifted splines in the full specified interval.

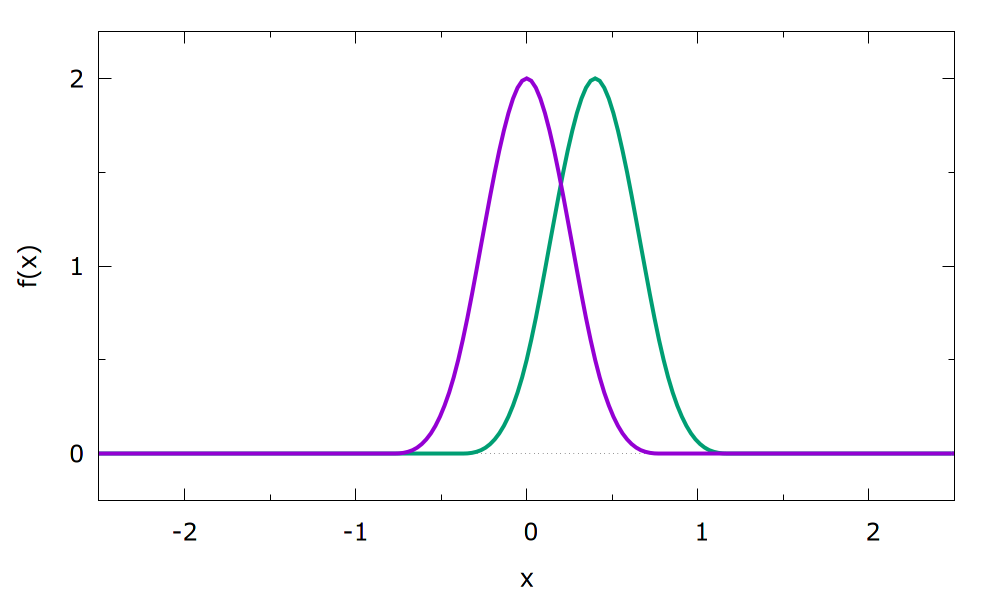
When the splines are used for a periodic CV (with the PERIODIC keyword), the sub-intervals are chosen in the same way, but only \(\text{ORDER}+1\) functions are required to fill it (the ones at the boundary coincide and the ones outside can be omitted).

To avoid 'blind' optimization of the basis functions outside the currently sampled area, it is often beneficial to use the OPTIMIZATION_THRESHOLD keyword of the VES_LINEAR_EXPANSION (set it to a small value, e.g. 1e-6)

Examples

The bias is expanded with cubic B splines in the intervall from 0.0 to 10.0 specifying an order of 20. This results in 24 basis functions.

Click on the labels of the actions for more information on what each action computes

bf: BF_CUBIC_B_SPLINES 
MINIMUM
compulsory keyword 
The minimum of the interval on which the basis functions are defined. 
=0.0 
MAXIMUM
compulsory keyword 
The maximum of the interval on which the basis functions are defined. 
=10.0 
ORDER
compulsory keyword 
The order of the basis function expansion. 
=20 The BF_CUBIC_B_SPLINES action with label bf

Glossary of keywords and components

Compulsory keywords

ORDER	The order of the basis function expansion.
MINIMUM	The minimum of the interval on which the basis functions are defined.
MAXIMUM	The maximum of the interval on which the basis functions are defined.

Options

DEBUG_INFO	( default=off ) Print out more detailed information about the basis set. Useful for debugging.
PERIODIC	( default=off ) Use periodic version of basis set.
NORMALIZATION	the normalization factor that is used to normalize the basis functions by dividing the values. By default it is 2.