The aim of this tutorial is to train users to perform and analyze metadynamics simulations with PLUMED. This tutorial has been prepared by Max Bonomi (adapting a lot of material from other tutorials) for the Master In Silico Drug Design, held at Universite' de Paris on October 26th, 2021.
Once this tutorial is completed users will be able to:
The TARBALL for this tutorial contains the following files:
diala.pdb: a PDB file for alanine dipeptide in vacuo.topol.tpr: a GROMACS run (binary) file to perform MD simulations of alanine dipeptide.do_block_fes.py: a python script to perform error analysis of metadynamics simulations.After dowloading the compressed archive to your local machine, you can unpack it using the following command:
tar xvzf master-ISDD-2.tar.gz
Once unpacked, all the files can be found in the master-ISDD-2 directory. To keep things clean, it is recommended to run each exercise in a separate sub-directory that you can create inside master-ISDD-2.
In the previous tutorial, we have seen that PLUMED can be used to compute collective variables (CVs) on a pre-calculated trajectory. However, PLUMED is most often use to add forces on the CVs during a MD simulation, for example, in order to accelerate sampling. To this aim, we have implemented a variety of possible biases acting on CVs. The complete documentation for all the biasing methods available in PLUMED can be found at the Bias page. In the following we will learn how to use PLUMED to perform and analyze a metadynamics simulation. Here you can find a brief recap of the metadynamics theory.
In metadynamics, an external history-dependent bias potential is constructed in the space of a few selected degrees of freedom \( \vec{s}({q})\), generally called collective variables (CVs) [67]. This potential is built as a sum of Gaussian kernels deposited along the trajectory in the CVs space:
\[ V(\vec{s},t) = \sum_{ k \tau < t} W(k \tau) \exp\left( -\sum_{i=1}^{d} \frac{(s_i-s_i({q}(k \tau)))^2}{2\sigma_i^2} \right). \]
where \( \tau \) is the Gaussian deposition stride, \( \sigma_i \) the width of the Gaussian for the \(i\)th CV, and \( W(k \tau) \) the height of the Gaussian. The effect of the metadynamics bias potential is to push the system away from local minima into visiting new regions of the phase space. Furthermore, in the long time limit, the bias potential converges to minus the free energy as a function of the CVs:
\[ V(\vec{s},t\rightarrow \infty) = -F(\vec{s}) + C. \]
In standard metadynamics, Gaussian kernels of constant height are added for the entire course of a simulation. As a result, the system is eventually pushed to explore high free-energy regions and the estimate of the free energy calculated from the bias potential oscillates around the real value. In well-tempered metadynamics [8], the height of the Gaussian is decreased with simulation time according to:
\[ W (k \tau ) = W_0 \exp \left( -\frac{V(\vec{s}({q}(k \tau)),k \tau)}{k_B\Delta T} \right ), \]
where \( W_0 \) is an initial Gaussian height, \( \Delta T \) an input parameter with the dimension of a temperature, and \( k_B \) the Boltzmann constant. With this rescaling of the Gaussian height, the bias potential smoothly converges in the long time limit, but it does not fully compensate the underlying free energy:
\[ V(\vec{s},t\rightarrow \infty) = -\frac{\Delta T}{T+\Delta T}F(\vec{s}) + C. \]
where \( T \) is the temperature of the system. In the long time limit, the CVs thus sample an ensemble at a temperature \( T+\Delta T \) which is higher than the system temperature \( T \). The parameter \( \Delta T \) can be chosen to regulate the extent of free-energy exploration: \( \Delta T = 0\) corresponds to standard MD, \( \Delta T \rightarrow\infty\) to standard metadynamics. In well-tempered metadynamics literature and in PLUMED, you will often encounter the term "bias factor" which is the ratio between the temperature of the CVs ( \( T+\Delta T \)) and the system temperature ( \( T \)):
\[ \gamma = \frac{T+\Delta T}{T}. \]
The bias factor should thus be carefully chosen in order for the relevant free-energy barriers to be crossed efficiently in the time scale of the simulation. Additional information can be found in the several review papers on metadynamics [66] [9] [108] [26]. To learn more: Summary of theory
We will play with a toy system, alanine dipeptide simulated in vacuo using the AMBER99SB-ILDN force field (see Fig. master-ISDD-2-ala-fig). This rather simple molecule is useful to understand data analysis and free-energy methods. This system is a nice example because it presents two metastable states separated by a high free-energy barrier. It is conventional use to characterize the two states in terms of Ramachandran dihedral angles, which are denoted with \( \phi \) (phi) and \( \psi \) (psi) in Fig. master-ISDD-2-transition-fig.
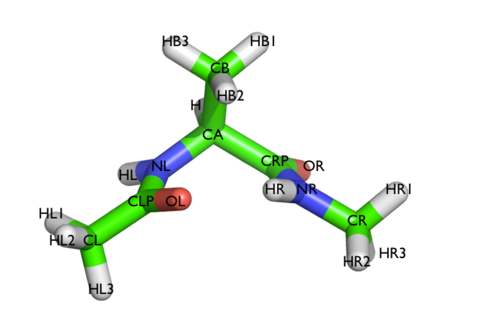
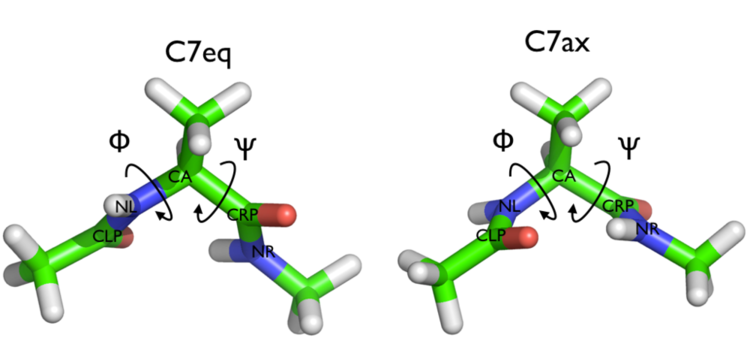
In this exercise we will setup and perform a well-tempered metadynamics run using the backbone dihedral \( \phi \) as collective variable. During the calculation, we will also monitor the behavior of the other backbone dihedral \( \psi \).
Here you can find a sample plumed.dat file that you can use as a template. Whenever you see an highlighted FILL string, this is a string that you must replace.

# Activate MOLINFO functionalities MOLINFOSTRUCTURE=diala.pdb # Compute the backbone dihedral angle phi, defined by atoms C-N-CA-C # you might want to use MOLINFO shortcuts phi: TORSIONcompulsory keyword a file in pdb format containing a reference structure.ATOMS=__FILL__ # Compute the backbone dihedral angle psi, defined by atoms N-CA-C-N # here also you might want to use MOLINFO shortcuts psi: TORSIONthe four atoms involved in the torsional angleATOMS=__FILL__ # Activate well-tempered metadynamics in phi metad: __FILL__the four atoms involved in the torsional angleARG=__FILL__ # Deposit a Gaussian every 500 time steps, with initial height equal to 1.2 kJ/molcould not find this keywordPACE=500could not find this keywordHEIGHT=1.2 # The bias factor should be wisely chosencould not find this keywordBIASFACTOR=__FILL__ # Gaussian width (sigma) should be chosen based on CV fluctuation in unbiased runcould not find this keywordSIGMA=__FILL__ # Gaussians will be written to file and also stored on gridcould not find this keywordFILE=HILLScould not find this keywordGRID_MIN=-picould not find this keywordGRID_MAX=pi ... # Print both collective variables on COLVAR file every 10 steps PRINTcould not find this keywordARG=__FILL__the input for this action is the scalar output from one or more other actions.FILE=COLVARthe name of the file on which to output these quantitiesSTRIDE=__FILL__compulsory keyword ( default=1 ) the frequency with which the quantities of interest should be output
The syntax for the command METAD is simple. The directive is followed by a keyword ARG followed by the labels of the CVs on which the metadynamics bias potential will act. The keyword PACE determines the stride of Gaussian deposition in number of time steps, while the keyword HEIGHT specifies the height of the Gaussian. For each CVs, one has to specify the width of the Gaussian by using the keyword SIGMA. Gaussian will be written to the file indicated by the keyword FILE.
In this example, the bias potential will be stored on a grid, whose boundaries are specified by the keywords GRID_MIN and GRID_MAX. Notice that you can provide either the number of bins for every CV (GRID_BIN) or the desired grid spacing (GRID_SPACING). In case you provide both PLUMED will use the most conservative choice (highest number of bins) for each dimension. In case you do not provide any information about bin size (neither GRID_BIN nor GRID_SPACING) and if Gaussian width is fixed, PLUMED will use 1/5 of the Gaussian width as grid spacing. This default choice should be reasonable for most applications.
Once your plumed.dat file is complete, you can run a 10-ns long metadynamics simulations with the following command:
> gmx mdrun -s topol.tpr -nsteps 5000000 -plumed plumed.dat
During the metadynamics simulation, PLUMED will create two files, named COLVAR and HILLS. The COLVAR file contains all the information specified by the PRINT command, in this case the value of the backbone dihedrals \( \phi \) and \( \psi \) every 10 steps of simulation. We can use gnuplot to visualize the behavior of the metadynamics CV \( \phi \) during the simulation:
gnuplot> p "COLVAR" u 1:2
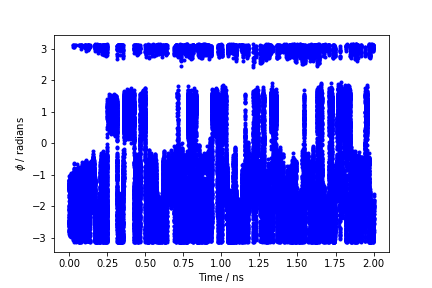
By inspecting Figure master-ISDD-2-phi-fig, we can see that the system is initialized in one of the two metastable states of alanine dipeptide. After a while (t=0.1 ns), the system is pushed by the metadynamics bias potential to visit the other local minimum. As the simulation continues, the bias potential fills the underlying free-energy landscape, and the system is able to diffuse in the entire phase space.
The HILLS file contains a list of the Gaussian kernels deposited along the simulation. If we give a look at the header of this file, we can find relevant information about its content:
#! FIELDS time phi sigma_phi height biasf #! SET multivariate false #! SET min_phi -pi #! SET max_phi pi
The line starting with FIELDS tells us what is displayed in the various columns of the HILLS file: the simulation time, the instantaneous value of \( \phi \), the Gaussian width and height, and the bias factor. We can use the HILLS file to visualize the decrease of the Gaussian height during the simulation, according to the well-tempered recipe:
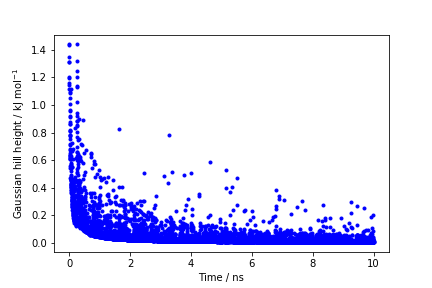
If we look carefully at the scale of the y-axis, we will notice that in the beginning the value of the Gaussian height is higher than the initial height specified in the input file, which should be 1.2 kJ/mol. In fact, this column reports the height of the Gaussian scaled by the pre-factor that in well-tempered metadynamics relates the bias potential to the free energy.
One can estimate the free energy as a function of the metadynamics CVs directly from the metadynamics bias potential. In order to do so, the utility sum_hills can be used to sum the Gaussian kernels deposited during the simulation and stored in the HILLS file.
To calculate the free energy as a function of \( \phi \), it is sufficient to use the following command line:
plumed sum_hills --hills HILLS
The command above generates a file called fes.dat in which the free-energy surface as function of \( \phi \) is calculated on a regular grid. One can modify the default name for the free-energy file, as well as the boundaries and bin size of the grid, by using the following sum_hills options:
--outfile - specify the outputfile for sumhills --min - the lower bounds for the grid --max - the upper bounds for the grid --bin - the number of bins for the grid --spacing - grid spacing, alternative to the number of bins
The result should look like this:
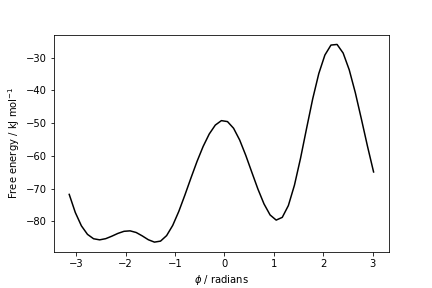
To give a preliminary assessment of the convergence of a metadynamics simulation, one can calculate the estimate of the free energy as a function of simulation time. At convergence, the reconstructed profiles should be similar. The sum_hills option --stride should be used to give an estimate of the free energy every N Gaussian kernels deposited, and the option --mintozero can be used to align the profiles by setting the global minimum to zero. If we use the following command line:
plumed sum_hills --hills HILLS --stride 100 --mintozero
one free energy is calculated every 100 Gaussian kernels deposited, and the global minimum is set to zero in all profiles. The resulting plot should look like the following:
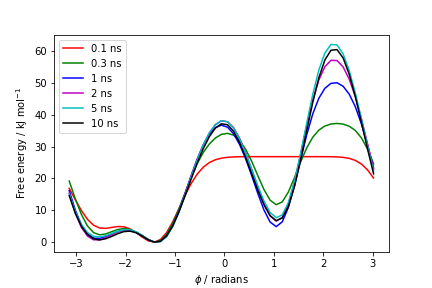
These two qualitative observations:
suggest that the simulation might be converged.
In the previous exercise we biased \(\phi\) and computed the free energy as a function of the same variable directly from the metadynamics bias potential using the sum_hills utility. However, in many cases you might decide which variable should be analyzed after having performed a metadynamics simulation. For example, you might want to calculate the free energy as a function of CVs other than those biased during the metadynamics simulation, such as the dihedral \( \psi \). At variance with standard MD simulations, you cannot simply calculate histograms of other variables directly from your metadynamics trajectory, because the presence of the metadynamics bias potential has altered the statistical weight of each frame. To remove the effect of this bias and thus be able to calculate properties of the system in the unbiased ensemble, you must reweight (unbias) your simulation.
There are multiple ways to calculate the correct statistical weight of each frame in your metadynamics trajectory and thus to reweight your simulation. For example:
In this exercise we will use the second method, which resembles the umbrella-sampling reweighting approach. In order to compute the weights we will use the driver tool.
First of all, you need to prepare a plumed_reweight.dat file that is identical to the one you used for running your metadynamics simulation except for a few modifications. First, you need to add the keyword RESTART=YES to the METAD command. This will make this action behave as if PLUMED was restarting, i.e. PLUMED will read from the HILLS file the Gaussians that have previously been accumulated. Second, you need to set the Gaussian HEIGHT to zero and the PACE to a large number. This will actually avoid adding new Gaussians (and even if they are added they will have zero height). Finally, you need to modify the PRINT statement so that you write every frame and that, in addition to phi and psi, you also write metad.bias. You might also want to change the name of the output file to COLVAR_REWEIGHT.

# Activate MOLINFO functionalities MOLINFOSTRUCTURE=diala.pdb __FILL__ # here goes the definitions of the phi and psi CVs # Activate well-tempered metadynamics in phi metad: __FILL__compulsory keyword a file in pdb format containing a reference structure.ARG=__FILL__ # Deposit a Gaussian every 10000000 time steps (never!), with initial height equal to 0.0 kJ/molcould not find this keywordPACE=10000000could not find this keywordHEIGHT=0.0 # <- this is the new stuff! # The bias factor should be wisely chosencould not find this keywordBIASFACTOR=__FILL__ # Gaussian width (sigma) should be chosen based on CV fluctuation in unbiased runcould not find this keywordSIGMA=__FILL__ # Gaussians will be written to file and also stored on gridcould not find this keywordFILE=HILLScould not find this keywordGRID_MIN=-picould not find this keywordGRID_MAX=pi # Say that METAD should be restarting (= reading an existing HILLS file)could not find this keywordRESTART=YES # <- this is the new stuff! ... # Print out the values of phi, psi and the metadynamics bias potential # Make sure you print out the 3 variables in the specified order at every step PRINTcould not find this keywordARG=__FILL__the input for this action is the scalar output from one or more other actions.FILE=COLVAR_REWEIGHTthe name of the file on which to output these quantitiesSTRIDE=__FILL__ # <- also change this one!compulsory keyword ( default=1 ) the frequency with which the quantities of interest should be output
Then run the driver tool using this command:
> plumed driver --mf_xtc traj_comp.xtc --plumed plumed_reweight.dat --kt 2.494339
Notice that you have to specify the value of \(k_BT\) in energy units. While running your simulation this information was communicated by the MD code.
As a result, PLUMED will produce a new COLVAR_REWEIGHT file with one additional column containing the metadynamics bias potential \( V(s) \) calculated using all the Gaussians deposited along the entire trajectory. The beginning of the file should look like this:
#! FIELDS time phi psi metad.bias #! SET min_phi -pi #! SET max_phi pi #! SET min_psi -pi #! SET max_psi pi 0.000000 -1.497988 0.273498 110.625670 1.000000 -1.449714 0.576594 110.873141 2.000000 -1.209587 0.831417 109.742353 3.000000 -1.475975 1.279726 110.752327
You can easily obtain the weight \( w \) of each frame using the expression \(w\propto\exp\left(\frac{V(s)}{k_BT}\right)\) (umbrella-sampling-like reweighting). At this point, you can read the COLVAR_REWEIGHT file using, for example, a python script and compute a weighted histogram. Alternatively, if you want PLUMED to do the weighted histograms for you, you can add the following lines at the end of the plumed_reweight.dat file:

# Use the metadynamics bias as argument as: REWEIGHT_BIASARG=__FILL__ # Calculate histograms of phi and psi dihedrals every 50 steps # using the weights obtained from the metadynamics bias potentials (umbrella-sampling-like reweighting) # Look at the manual to understand the parameters of the HISTOGRAM action! hhphi: HISTOGRAMcompulsory keyword ( default=*.bias ) the biases that must be taken into account when reweightingARG=phithe input for this action is the scalar output from one or more other actions.STRIDE=50compulsory keyword ( default=1 ) the frequency with which the data should be collected and added to the quantity being averagedGRID_MIN=-picompulsory keyword the lower bounds for the gridGRID_MAX=picompulsory keyword the upper bounds for the gridGRID_BIN=50the number of bins for the gridBANDWIDTH=0.05compulsory keyword the bandwidths for kernel density estimationLOGWEIGHTS=as hhpsi: HISTOGRAMlist of actions that calculates log weights that should be used to weight configurations when calculating averagesARG=psithe input for this action is the scalar output from one or more other actions.STRIDE=50compulsory keyword ( default=1 ) the frequency with which the data should be collected and added to the quantity being averagedGRID_MIN=-picompulsory keyword the lower bounds for the gridGRID_MAX=picompulsory keyword the upper bounds for the gridGRID_BIN=50the number of bins for the gridBANDWIDTH=0.05compulsory keyword the bandwidths for kernel density estimationLOGWEIGHTS=as # Convert histograms h(s) to free energies F(s) = -kBT * log(h(s)) ffphi: CONVERT_TO_FESlist of actions that calculates log weights that should be used to weight configurations when calculating averagesGRID=hhphi ffpsi: CONVERT_TO_FEScompulsory keyword the action that creates the input grid you would like to useGRID=hhpsi # Print out the free energies F(s) to file once the entire trajectory is processed DUMPGRIDcompulsory keyword the action that creates the input grid you would like to useGRID=ffphicompulsory keyword the action that creates the grid you would like to outputFILE=ffphi.dat DUMPGRIDcompulsory keyword ( default=density ) the file on which to write the grid.GRID=ffpsicompulsory keyword the action that creates the grid you would like to outputFILE=ffpsi.datcompulsory keyword ( default=density ) the file on which to write the grid.
and plot the result using gnuplot:
gnuplot> p "ffphi.dat" u 1:2 w lp gnuplot> p "ffpsi.dat" u 1:2 w lp
You can now compare the free energies as a function of \( \phi \) calculated:
The results should be identical (see Fig. master-ISDD-2-fescomp-fig).
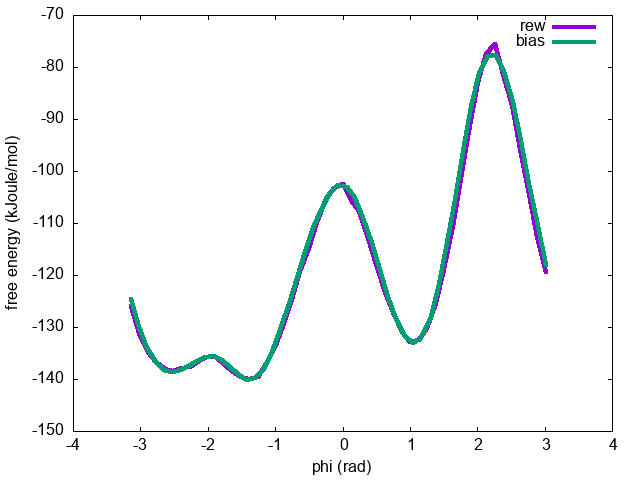
.
In the previous exercise, we calculated the final bias \( V(s) \) on the entire metadynamics trajectory and we used this quantity to calculate the correct statistical weight of each frame that we need to reweight the biased simulation. In this exercise, we will see how this information can be used to calculate the error in the reconstructed free energies and assess whether our simulation is converged or not. Let's first calculate the un-biasing weights \(w\propto\exp\left(\frac{V(s)}{k_BT}\right)\) from the COLVAR_REWEIGHT file obtained at the end of Exercise 3: Reweighting (unbiasing) a metadynamics simulation:
# Find maximum value of bias to avoid numerical errors when calculating the un-biasing weights
bmax=`awk 'BEGIN{max=0.}{if($1!="#!" && $4>max)max=$4}END{print max}' COLVAR_REWEIGHT`
# Print phi values and un-biasing (un-normalized) weights
awk '{if($1!="#!") print $2,exp(($4-bmax)/kbt)}' kbt=2.494339 bmax=$bmax COLVAR_REWEIGHT > phi.weight
If you inspect the phi.weight file, you will see that each line contains the value of the dihedral \( \phi \) along with the corresponding (un-normalized) weight \( w \) for each frame of the metadynamics trajectory:
0.907347 0.0400579 0.814296 0.0169656 1.118951 0.0651276 1.040781 0.0714174 1.218571 0.0344903 1.090823 0.0700568 1.130800 0.0622998
At this point we can apply the block-analysis technique (for more info about the theory, have a look at Trieste tutorial: Averaging, histograms and block analysis) to calculate the average free energy across the blocks and the error as a function of block size. For your convenience, you can use the do_block_fes.py python script to read the phi.weight file and produce the desired output. We use a bash loop to test block sizes ranging from 1 to 1000:
# Arguments of do_block_fes.py # - input file with CV value and weight for each frame of the trajectory: phi.weight # - number of CVs: 1 # - CV range (min, max): (-3.141593, 3.141593) # - # points in output free energy: 51 # - kBT (kJoule/mol): 2.494339 # - Block size: 1<=i<=1000 (every 10) # for i in `seq 1 10 1000`; do python3 do_block_fes.py phi.weight 1 -3.141593 3.141593 51 2.494339 $i; done
For each value of block size N, you will obtain a separate fes.N.dat file, containing the value of the \( \phi \) variable on a grid, the average free energy across the blocks with its associated error (in kJ/mol) on each point of the grid:
-3.141593 23.184653 0.080659 -3.018393 17.264462 0.055181 -2.895194 13.360259 0.047751 -2.771994 10.772696 0.043548 -2.648794 9.403544 0.042022
Finally, we can calculate the average error along each free-energy profile as a function of the block size:
for i in `seq 1 10 1000`; do a=`awk '{tot+=$3}END{print tot/NR}' fes.$i.dat`; echo $i $a; done > err.blocks
and visualize it using gnuplot:
gnuplot> p "err.blocks" u 1:2 w lp
As expected, the error increases with the block size until it reaches a plateau in correspondence of a dimension of the block that exceeds the correlation between data points (Fig. master-ISDD-2-block-phi).
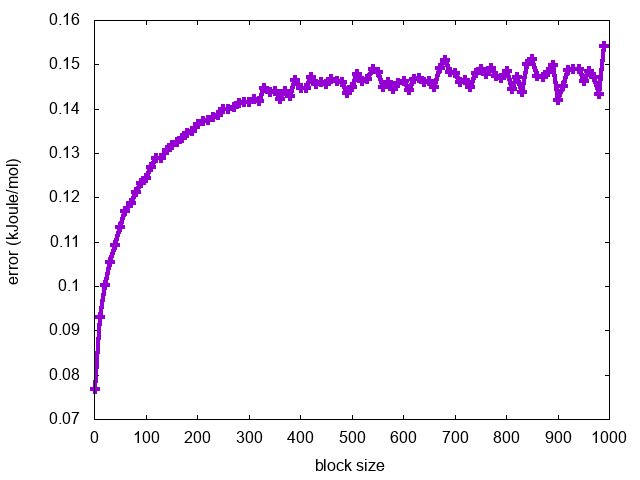
What can we learn from this analysis about the convergence of the metadynamics simulation?
In summary, in this tutorial you should have learned how to use PLUMED to: